vptree实现经纬度转省市地址

手机定位的经纬度转成省市区地址信息，其实是一个平面2D求最近点的算法问题，可以简单理解为将中国地图密密麻麻插面小图钉，当需要知道某个经纬度的地理位置时，只需要计算它离哪个小图钉最近，用这个最近小图钉的位置来估计该经纬度的省市区信息。

首先需要获取POI数据，POI数据越精细越好，越精细就能定位到用户当前所在哪条街，哪条路，哪橦楼里，当然数据量越大，带来的硬件资源开销也越大。遍布中国地图的POI数据，光小区、大楼、公路相关，大约在千万量级。

接着实现一套最小距离计算算法，整个系统就完成了。近邻搜索，或者叫k近邻算法，也就是k-Nearest Neighbor(KNN)，是最简单的机器学习算法，常见算法有kd-tree和vp-tree，vp-tree算法相比与kd-tree算法有更好的适应性，能解决高维问题。经纬度转省市区问题属于二维空间问题，所以两种算法均可，但我选择了vp-tree。

vp-tree的算法原理很简单，即：定义距离函数D(x, y)，表示x点和y点的距离，那么有 D(x, y) <= D(x, z) + D(z, y)。其实就是简单的三角关系，两边之和大于第三边，三点成直线时，等号成立。这里的距离不一定要是几何距离（欧几里德距离），只要满足非负、对称、两边之和大于等于第三边即可，常见有：汉明距离、编辑距离、曼哈顿距离、余弦相关系数、皮尔逊系数等。

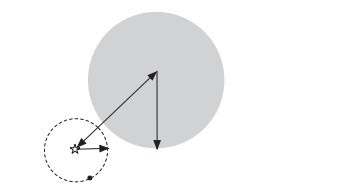
建树过程，或者叫学习过程：选择一个制高点（Vantage Point），然后计算余下每个点与该点的距离，将距离排序，选择中间距离MidD，于是距离小于MidD的点归到左子树，大于等于MidD的点归到右子树，然后再对左子树和右子树分别进行如上操作。为了加快建树效率，可以将排序后的点分成多份，形成多叉树。对制高点的选择不同，建树不同，效率也不同，需要根据实际情况考虑。

查询过程，或者叫训练过程：计算查询点p与树的分叉点vp的距离Dis，当距离小于MidD时，那么，p与右子树的最小距离为MidD - Dis，p与左子树的最小距离为0，p与vp的距离为Dis，此三种情况置于小根堆中，依次pop小根堆的最小值，如果是子树，重复上面的计算过程，如果是vp点，此vp点就是要查找的最近的点。 

通常认为距离计算函数D(x, y)是最耗时的，所以能减少距离函数的调用次数，就能有效加快在线查询。这就涉及到vp-tree的剪枝问题，在建树时其实计算了每个点与所有它的父结点的距离，而在查询时，查询点也是依次与当前vp点的所有父结点进行过距离计算，这是两个等长的向量V1和V2，所以查询点p与某子树的最小距离>=max(|V1 - V2|)。此外，我们往往只关心一定范围内的近邻点，比如10公里范围内的，在放入小根堆前做一下判断，提前剔除掉，能够减少小根堆的存储消耗。